
In the limit as the vertices go to infinity, there are even ideal hyperbolic triangles in which all three angles are 0°. In this article, the two limiting lines are called asymptotic and lines sharing a common perpendicular are called ultraparallel the simple word parallel may apply to both.Ī characteristic property of hyperbolic geometry is that the angles of a triangle add to less than a straight angle. The strong parallel postulate easily implies Euclid 5, and Euclid 5 also implies the strong. We completely settle the questions about implications between the three versions of the parallel postulate. Models have been constructed within Euclidean geometry that obey the axioms of hyperbolic geometry, thus proving that the parallel postulate is independent of the other postulates of Euclid.īecause there is no precise hyperbolic analogue to Euclidean parallel lines, the hyperbolic use of parallel and related terms varies among writers. The first main result of this paper is that Euclid 5 suffices to define coordinates, addition, multiplication, and square roots geometrically. In hyperbolic geometry there are at least two distinct lines through P which do not intersect R, so the parallel postulate is false. The parallel postulate in Euclidean geometry is equivalent to the statement that, in two-dimensional space, for any given line R and point P not on R, there is exactly one line through P that does not intersect R i.e., that is parallel to R.
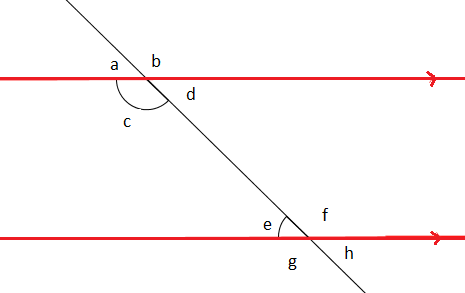
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced. the definition of parallel lines together with the axioms of neutral geometry.

Freebase (0.00 / 0 votes) Rate this definition: the real content of the Euclidean Parallel Postulate is the statement.


 0 kommentar(er)
0 kommentar(er)
